I/D #2: Unit O: How can we derive the patterns for our special right triangles?

Inquiry Activity Summary:
1. 30-60-90 triangle
To derive the pattern for 30-60-90 triangles, we need to look at equilateral triangle, which has all equal side lengths and angle degrees. In this case, all sides are equal to 1. When we cut it down the middle, it splits the triangle into two 30-60-90 triangles.

 

Using the Pythagorean theorem to find our missing leg length, we plug in our values to get (1/2)^2+ b^2= (1)^2. The (1/2) came from the one side length that got cut into two. The (1) length would be our hypotenuse, which was already given to us. Now we solve for b to get √3/2

Now because we do not want any fractions to make things complicated, we multiply all the leg lengths by 2 to get "prettier" numbers.

Because we want to be able to apply this pattern for all 30-60-90 triangles with different side lengths, we need to use a variable to allow for the same ratios as the triangle with side lengths of 1.

2. 45-45-90 triangle
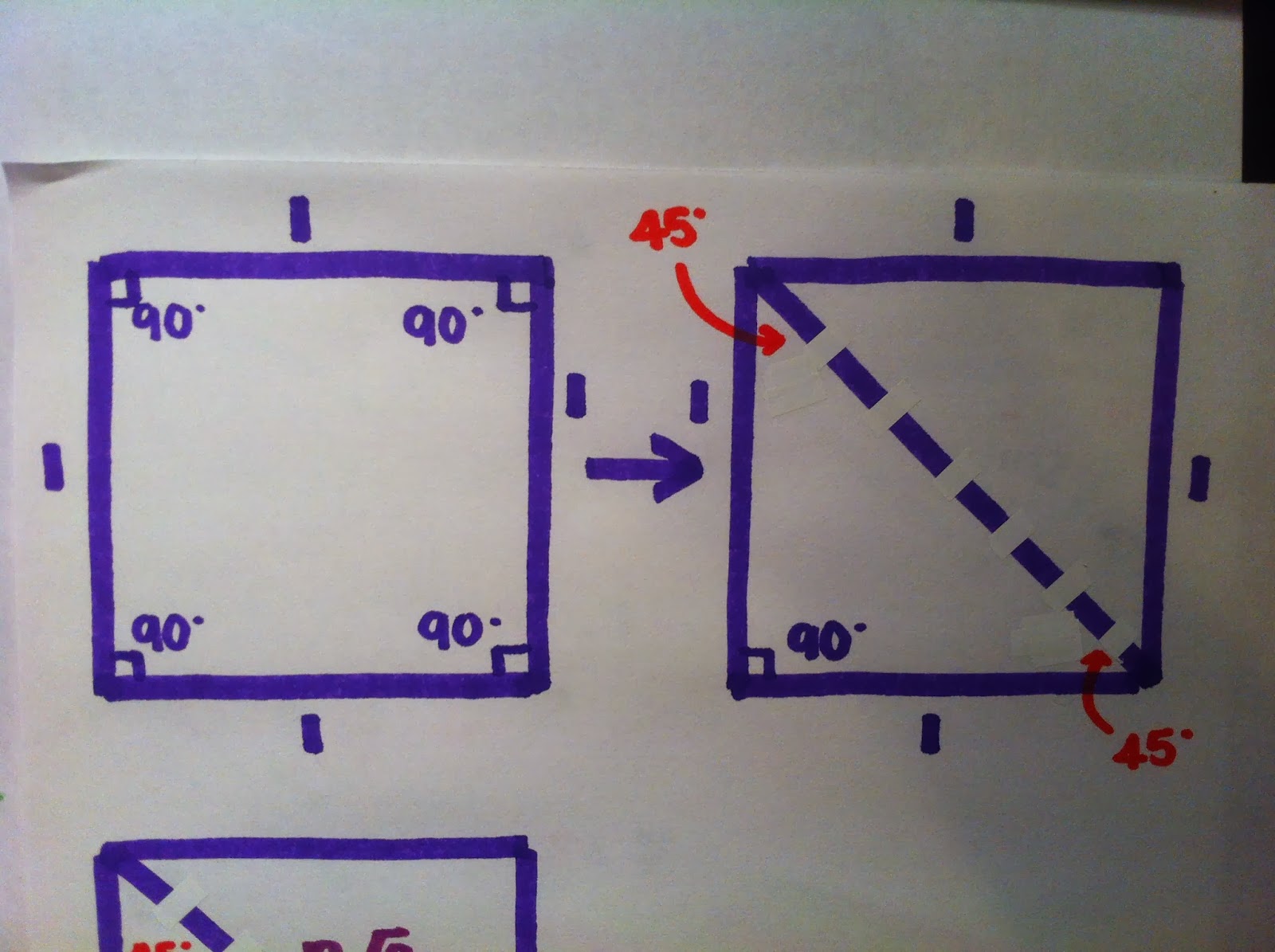
To derive the pattern for 45-45-90 triangles, we need to look at squares, which has all equal side lengths and angle degrees. In this case, all sides are equal to 1. When we cut it diagonally, it splits into two 45-45-90 triangles.

Using the Pythagorean theorem to find our missing leg length, we plug in our values to get (1)^2+ (1)^2= c^2. The (1) lengths would be our two legs, which was already given to us. Now we solve for c to get √2.

Because we want to be able to apply this pattern for all 45-45-90 triangles with different side lengths, we need to use a variable to allow for the same ratios as the triangle with side lengths of 1.

 

 

Inquiry Activity Reflection

 

1. Something I never noticed before about special right triangles is that the ratios came from the Pythagorean theorem.

2. Being able to derive these triangles myself aids in my learning because I now completely understand the rules of special right triangles. Through this activity, I understand where these values come from.