BQ #7: Deriving the Difference Quotient

The difference quotient, f(x+h)-f(x)/h, is the slope of a secant line, which seems more complicated than the regular slope of y2-y1/ x2-x1, or rise over run. But it's not all that complicated. The complex difference quotient actually comes from the simple slope equation.
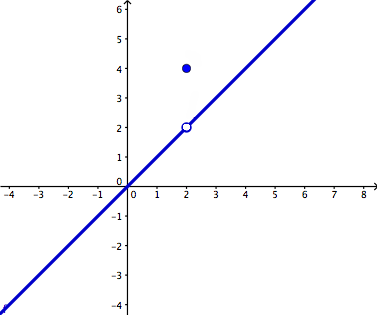
Now to find the slope of a line, we need to know 2 points on the graph, represented by (x,y). Now we replace that first y with f(x) to give us (x, f(x)) and replace the second x and y with (x+h), f(x+h). Now if we were to use the slope formula we would get:
f(x+h)-f(x)/(x+h)-x. And like any other algebraic problem, we simplify, canceling the x's on the bottom, giving us the difference quotient. 

Now you know where the difference quotient comes from. However, in calculus, we proceed further, to find what is known as derivatives. When finding the derivative, all possible tangent lines of a graph, you would find the limit as h approaches 0. But why 0? A tangent line touches a graph only once, while the secant line  touches the graph TWICE. So, in order for us to get one point, we can basically have those two points on top of each other... meaning that they are in the same place. We are able to get them to sit on top of each other by decreasing the "h", the distance between the two points. The smaller "h" is the closer the two points are. Therefore, we have our limit as h approaches 0 because we can't actually have it at 0, but we can get it pretty darn close.  

For a visual, go watch this video:

                            https://www.youtube.com/watch?v=XA0fZh8cXV8

BQ #6: Unit U

1. What is continuity? What is discontinuity?

Continuity is when the graph is predictable, has no breaks, jumps, or holes, could be drawn without lifting the pencil, and has the same value as the limit.

http://www.analyzemath.com/calculus/continuity/continuous_1.gif

Discontinuity is the opposite: it is unpredictable, does have breaks, jumps, and holes, cannot be drawn without lifting the pencil, and varies if the value and the limit are the same. There are two families of discontinuities: removable and non-removable. A point discontinuity is the removable discontinuity, which is also known has the hole. There are three types of non-removable discontinuities: jump, which shows a "jump" or space between the function, infinite, which is also known as unbounded behavior and occurs where there is a vertical asymptote, and oscillating behavior, which shows the function as a condensed set of "wiggles".


 

Point discontinuity
http://dj1hlxw0wr920.cloudfront.net/userfiles/wyzfiles/4a69dec7-03e0-492f-ac16-4dcd555579c9.gif

 

Jump Discontinuity
http://image.tutorvista.com/content/feed/u364/discontin.GIF
 

Infinite Discontinuity
http://image.tutorvista.com/cms/images/67/inv-function-eg.JPG

Oscillating behavior
http://www.cwladis.com/math301/lecture%20images/infiniteoscillationdiscontinuityat1.gif

 

2. What is a limit? When does a limit exist? When does a limit not exist? What is the difference between a limit and a value?

A limit is the intended height of a function and is read as "the limit as x approaches 'a number' of f(x) is equal to 'L' ". A limit exists as long as you reach the same height from both the left and the right direction. If the graph does not break at a given x-value, then the limit will exist there. This means that a limit will exists in functions with holes. However, a limit will not be reached in non-removable discontinuities such as jumps, infinite discontinuities, or oscillating behavior. For jumps, the limit does not exist because the function has different left/right heights. For infinite discontinuities, the limit does not exist because of unbounded because due to vertical asymptotes.  However, we can still write one-sided limits. While limit is the intended height, the value is the actual height. This means that the limit and value can be the same or different depending on the function. Sometimes, there may be no actual value, as in the case with 2 open circles.

  http://00.educdn.com/files/static/mcgrawhillprof/9780071624756/LIMITS_AND_CONTINUITY_RAPID_REVIEW_02.GIF

As you can see here, the open circle (which is the limit) is different from the closed circle (which is the value).

3. How do we evaluate limits numerically, graphically, and algebraically?

To evaluate limits numerically, you will have to begin by drawing a table with 3 left and 3 right of number x is approaching. The values on the ends should be a tenth away from the center, and the closer you get to the center, the closer you get to the x-value. You would then plug the function into your graphing calculator and could either trace the location of the x-value or solve the function. An example can be seen below.

http://people.hofstra.edu/stefan_waner/realworld/tutorials/frames2_6a.html

To evaluate limits graphically, "plug the function into the y= screen on your graphing calculator. Then you can either go to 'tblset', make your independent variable 'ask', go to table, and then type in the values close to the limit. Or you could go to 'graph, hit 'trace', and trace to the value you are looking for" (Kirch). To find the limit, put your finger on a spot to the left and to the right of where you want to evaluate the limit and then move them together to find where they meet. If they don't, then there is no limit.
                          https://www.youtube.com/watch?v=_IT4hSM9DjA

When solving for limits algebraically, you need to begin with the direct substitution method. Like the name, all you need to do is take the number the limit is approaching and plug it in anywhere you see x. Through substitution, we can get 4 types of answers:
1. numerical answer
2. 0/#, which is 0
3. #/0 which is undefined and the limit does not exist
4. 0/0 indeterminate form

                          https://www.youtube.com/watch?v=1AKrjrl6Xpw


Now, if we end up with an indeterminate form, we must use another method to solve for the limit. The first one we could try out is the dividing out/ factoring method. You factor both the numerator and denominator and cancel out the common terms to remove the 0 in the denominator. Then once again, you use substitution with the simplified expression.

                        https://www.youtube.com/watch?v=zpcBkRpqHqQ

Now if you are unable to factor out, you will have to use the rationalizing/conjugate method. First you multiply the top and bottom by the conjugate (whichever term has the RADICAL). Then you simplify by foiling the value that was used to find the conjugate but leaving the other FACTORED. Then cancel out common terms, and substitute the simplified function to find the limit.

                          https://www.youtube.com/watch?v=WVj284EvgBI

 

 

 

BQ #3: Unit T Concepts 1-3

How do the graphs of sine and cosine relate to each of the others?Emphasize asymptotes in your response.

1. Tangent
With tangent, we know that the unit circle ratio would be sine over cosine. If we would put that into variables, y over x. When we look at how sine and cosine graphs relate to tangent, we notice that if both sine and cosine are positive, then tangent would be positive; if one is negative, then tangent is negative; if both are negative, then tangent is positive. That is basic division rules. Unlike sine and cosine, tangent graphs have asymptotes (which are areas that we cannot touch; undefined). What we need to realize is that the sine over cosine ratio is responsible for those asymptotes: if we divide any number by 0, it would come out as undefined. If cosine (x) were to be equal to 0, that would result in an asymptote. If we were to look at a unit circle, we should know that the x value would equal 0 at 90 degrees and 270 degrees. Converting back to the tangent graph and radians, we know that our asymptotes would be at pi/2 and 3pi/2.

                    https://www.desmos.com/calculator/hjts26gwst

2. Cotangent
With cotangent, we face the reciprocal unit circle ratio of cosine over sine, or x over y. When we look at how cosine and sine graphs relate to tangent, we notice that if both cosine and sine are positive, then cotangent would be positive; if one is negative, then cotangent is negative; if both are negative, then cotangent is positive. Unlike cosine and sine, cotangent graphs also have asymptotes Cotangent graphs are identically related to cosine and sine as its reciprocal, but have different asymptotes. If sine (y) were to be equal to 0, that would result in an asymptote. If we were to look at a unit circle, we should know that the y value would equal 0 at 0 degrees and 180 degrees. Converting back to the cotangent graph and radians, we know that our asymptotes would be at 0 and pi.

https://www.desmos.com/calculator/hjts26gwst

3. Secant
Unlike tangent and cotangent, secant is only related to the cosine graph. The unit circle ratio of secant is 1/cosine. If cosine were to have positive values on its graph, so would secant, and vice versa. Because secant is the reciprocal of cosine, we notice that if we were to have a low value on the cosine graph, the reciprocal of that value would be bigger on the secant graph, and vice versa. We should also notice that each curve of the secant graphs touch the "mountains" and "valleys" of the cosine graph. Looking at a graph, if we were to have a value of 0 on the cosine graph (0/1), we should know that that is where our asymptotes would be for the secant graph(1/0 = undefined).

                 https://www.desmos.com/calculator/hjts26gwst

4. Cosecant
Again, unlike tangent and cotangent, cosecant is only related to the sine graph. The unit circle ratio of cosecant is 1/sine. If sine were to have positive values on its graph, so would cosecant, and vice versa. Because cosecant is the reciprocal of sine, we notice that if we were to have a low value on the sine graph, the reciprocal of that value would be bigger on the cosecant graph, and vice versa. We should also notice that each curve of the cosecant graphs touch the "mountains" and "valleys" of the sine graph. Looking at a graph, if we were to have a value of 0 on the sine graph (0/1), we should know that that is where our asymptotes would be for the cosecant graph(1/0 = undefined).

 

https://www.desmos.com/calculator/hjts26gwst

 

 

BQ #4: Unit T Concept 3

Why is a “normal” tangent graph uphill, but a “normal” cotangent graph downhill? Use unit circle ratios to explain.

If we refer to the unit circle and ASTC, we know that tangent and cotangent are positive in quadrants 1 and 3 and negative in quadrants 2 and 4. If we were to break apart the unit circle into a line, we would get + - + - values for both trig functions. And unlike the other trig functions, tangent and cotangent have a period of pi rather than 2pi.

Tangent has the ratio of sin/cos (y/x), so we get asymptotes whenever cosine is equal to zero. On the unit circle, that would be the values of pi/2 and 3pi/2. If we were to draw out the graph, we notice that it goes "uphill" because each asymptote compresses an area where the graph would start with negative values and into positive values.

Cotangent has the ratio of cos/sin (x/y), so we get asymptotes whenever sine is equal to zero. On the unit circle, that would be the values of 0 and pi. If we were to draw out the graph, we would notice that it goes "downhill" because each asymptote compresses an area where the graph would start with positive values and into negative values.

BQ #5: Unit T Concepts 1-3

Why do sine and cosine NOT have asymptotes, but the other four trig graphs do? Use unit circle ratios to explain.

Sine and cosine do not have asymptotes because their ratios: y/r and x/r. This means that the radius (r) will always be equal 1, and will never have a 0 as the denominator. Sine and cosine will not encounter asymptotes because we will never have an undefined answer (0 divided by any number).

Unlike sine and cosine, the other four trig graphs do include asymptotes. Cosecant has a ratio of r/y. The "y" value can be 0 in :(1,0) or (-1,0). Secant has a ratio of r/x and x can be 0 in : (0,1) and (0, -1). Cotangent and tangent have the ratios of x/y and y/x, which means either numerator can have the value of 0.

A crucial thing to remember is that cotangent and and cosecant have the same denominator in their ratios (y), which means they will have the same asymptotes. Tangent and secant will have the same asymptotes because their denominators in their ratios (x).

BQ #2: Unit T Concept Intro

How do the trig graphs relate to the Unit Circle?

Period? - Why is the period for sine and cosine 2pi, whereas the period for tangent and cotangent is pi?

When we refer back to the Unit Circle involving sine, cosine, and tangent, we remember ASTC to remember which trig function is positive for each quadrant.

If we refer to ASTC for sine, we know that the function would be positive in quadrants 1 and 2, and negative in quadrants 3 and 4. This creates the repetition of + + - -. When dealing with periods, we have to have a completed pattern. And since it takes the whole unit circle, which equals 2pi, to make that pattern repeat itself, the period is 2pi.

                                  http://www.regentsprep.org/Regents/math/algtrig/ATT5/sine77.gif

This idea also goes for cosine. The function is positive in quadrants 1 and 4, and negative in quadrants 2 and 3. This gives us the repetition of + - - +. Because it does not have a repeating pattern, a cosine period is also 2pi.
 

 

    http://www.regentsprep.org/Regents/math/algtrig/ATT5/unitcirclecowine.gif

Unlike sine and cosine, a tangent period is only pi. Referring to ASTC, tangent is positive in quadrants 1 and 3 and negative in quadrants 2 and 4, which gives us the pattern of + - + -. Comparing to sine and cosine, we already have a pattern, but instead of going all the way around the unit circle for a period, we only need to go half way, or pi.

                                        http://www.clarku.edu/~djoyce/trig/tan.gif

Amplitude? – How does the fact that sine and cosine have amplitudes of one (and the other trig function)relate to what we know about the unit circle?

Amplitudes are half the distance between the highest and the lowest points on the sine and cosine graphs. Sine has the ratio of y/r and cosine has the ratio of x/r. R can only equal 1 (the radius of a unit circle is 1), which means the values x and y can only go up to 1. When dealing with the value of sine and cosine, we should know that sine and cosine have a value range of -1 to 1; anything out of that range would leave the trig function undefined. Now we look at other trig functions: tangent is y/x. We are not restricted to value range of -1 and 1 because we can divide by any other number. Cotangent is the reciprocal (x/y) of tangent. For cosecant and secant, they have the ratios of r/y and r/x. You can divide your "r", which is 1, by a smaller number, and get any value bigger than -1 or 1. That is why those other functions do not have amplitudes, but instead asymptotes.

Reflection #1: Unit Q: Verifying Identities

1.What does it actually mean to verify a trig identity?

To verify a trig function means to have a different version of the same trig function. We could have different trig functions in equations or fractions, but eventually reduces to one trig function.

2.What tips and tricks have you found helpful?

To get through this unit, it is crucial to memorize all the trig identities. It was easy to do because we had already learned and memorized all the reciprocal identities from a past unit. Also remember that reciprocal and ratio identities are able to power up or down, but not Pythagorean identities.

3.Explain your thought process and steps you take in verifying a trig identity.  Do not use a specific example, but speak in general terms of what you would do no matter what they give you.

To get through to verify a trig function, the first thing I do is look for any identities to simplify the function. I would look for any greatest common factors, cancel out, combine like terms, or it dealing with fractions, I would multiply the fraction by the conjugate to get a common denominator. If there are any tan or cot functions, I could use ratio identities to convert them to sin and cos, but one thing I remember is not to square anything because I am only allowed to square both sides.