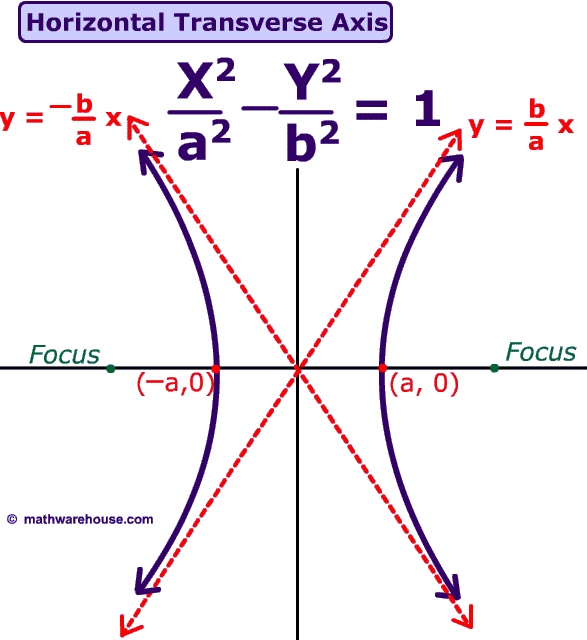
2. Algebraically and graphically, a hyperbola was look like this:
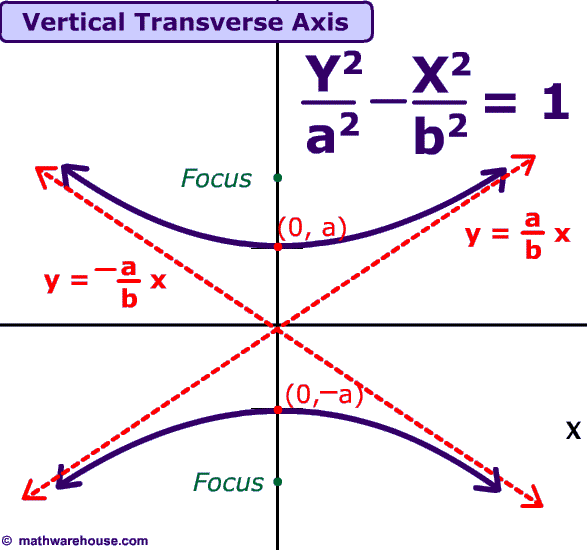
or like this:
(http://www.mathwarehouse.com/hyperbola/images/picture-of-hyperbola-vertical-transverse.gif)
For graphing each hyperbola, the direction depends on whether the "y" or "x" is negative. If the "y" is negative, then the hyperbolas will have a left and right direction (picture 1). If the "x" is negative, then the hyperbolas will have an up and down direction (picture 2).
The key features of hyperbolas are: center, transverse axis, conjugate axis, vertices, co-vertices, foci, eccentricity, and asymptotes. To find the center, we need to remember : "h" goes with "x" and "k" goes with "y". Going into our standard form, we find our "h" and our "k", our center (h,k). You can plot the center, and go on from there.
Looking at standard form, whichever term ("x" or "y") comes first will determine whether your transverse axis is horizontal or vertical. If "y" is the negative term, that tells us that our transverse axis will be horizontal. If "x" is the negative term, that tells us that our transverse axis will be vertical. Knowing this, we will know that our conjugate axis must be the opposite. So if our transverse axis is vertical, our conjugate axis will be horizontal and vice versa. (Side note: By knowing if the axes are horizontal or vertical, we will know if our lines will be "x=" or "y=". And because we know our axes go through our center, we know those "x=h" and "y=k".) The distance of the transverse axis is 2a ("a" is the square root of the denominator beneath the first term) and the distance of the conjugate is 2b ("b" is the square root of the denominator beneath the second term). To determine your transverse and conjugate axes graphically, look at the branches. If your branches go left and right, your transverse axis is horizontal. If your branches go up and down, your transverse axis is vertical. If you want to know the length of either of the axes, simply count the units (to find "a" or "b", divide the entire length of the axis by 2).
Graphically, the vertices are the ends of the transverse axis; just look at the end points and you have the vertices. Algebraically, all you need to know is what your "a" is. If your transverse axis is "x=" then you know that the "x's" in your vertices will remain the same as your center. From there, all you need to do is add and subtract "a" to "k". The same would for the co-vertices. Look for the end points of the conjugate axis on your graph. Algebraically, find "b" and add that to the value that is changing ("x" or "y").
Your foci is the same idea, with the adding to either the "x" or "y" values of your center (because your foci are "c" units away from your center). The focus will always be on the transverse axis long side the vertices.
The key features of hyperbolas are: center, transverse axis, conjugate axis, vertices, co-vertices, foci, eccentricity, and asymptotes. To find the center, we need to remember : "h" goes with "x" and "k" goes with "y". Going into our standard form, we find our "h" and our "k", our center (h,k). You can plot the center, and go on from there.
Looking at standard form, whichever term ("x" or "y") comes first will determine whether your transverse axis is horizontal or vertical. If "y" is the negative term, that tells us that our transverse axis will be horizontal. If "x" is the negative term, that tells us that our transverse axis will be vertical. Knowing this, we will know that our conjugate axis must be the opposite. So if our transverse axis is vertical, our conjugate axis will be horizontal and vice versa. (Side note: By knowing if the axes are horizontal or vertical, we will know if our lines will be "x=" or "y=". And because we know our axes go through our center, we know those "x=h" and "y=k".) The distance of the transverse axis is 2a ("a" is the square root of the denominator beneath the first term) and the distance of the conjugate is 2b ("b" is the square root of the denominator beneath the second term). To determine your transverse and conjugate axes graphically, look at the branches. If your branches go left and right, your transverse axis is horizontal. If your branches go up and down, your transverse axis is vertical. If you want to know the length of either of the axes, simply count the units (to find "a" or "b", divide the entire length of the axis by 2).
Graphically, the vertices are the ends of the transverse axis; just look at the end points and you have the vertices. Algebraically, all you need to know is what your "a" is. If your transverse axis is "x=" then you know that the "x's" in your vertices will remain the same as your center. From there, all you need to do is add and subtract "a" to "k". The same would for the co-vertices. Look for the end points of the conjugate axis on your graph. Algebraically, find "b" and add that to the value that is changing ("x" or "y").
Your foci is the same idea, with the adding to either the "x" or "y" values of your center (because your foci are "c" units away from your center). The focus will always be on the transverse axis long side the vertices.
"Eccentricity is a measure of how much the conic section deviates from being circular" (Kirch). For a hyperbola, it must be greater than 1. Algebraically, to find the eccentricity, we use the formula "e=c/a."
Unlike the other conics, hyperbolas have asymptotes (restrictions). To find the asymptotes algebraically, we use between two formulas depending on the direction of the transverse axis. If it is horizontal, then we use y= k± b/a (x-h). If it is vertical, then it is y=k± a/b (x-h). On a graph, you will notice the two dotted lines making an X going through the center and corners of the box: that would be your asymptotes. Notice how the hyperbolas are drawn really close to them, but never touches!
If you need an example to put all of this information together, here is a video to help you visually!
(http://www.youtube.com/watch?v=Z6cwpsDC_5A)
Unlike the other conics, hyperbolas have asymptotes (restrictions). To find the asymptotes algebraically, we use between two formulas depending on the direction of the transverse axis. If it is horizontal, then we use y= k± b/a (x-h). If it is vertical, then it is y=k± a/b (x-h). On a graph, you will notice the two dotted lines making an X going through the center and corners of the box: that would be your asymptotes. Notice how the hyperbolas are drawn really close to them, but never touches!
If you need an example to put all of this information together, here is a video to help you visually!
3. Real world applications of hyperbolas can be seen in cooling towers for nuclear reactors. When building cooling towers, there were problems in creating a building that would be able to "withstand high winds" and "intense conditions with as little material as possible". (http://www.pleacher.com/mp/mlessons/calculus/apphyper.html) Eventually, engineers discovered the benefits of creating these towers into the shape of a 3D hyperbola.
By building these towers into hyperboloids, they are able to stand up to high winds and use less material. "A 500 foot tower can be made of a reinforced concrete shell only six to eight inches wide." (http://www.pleacher.com/mp/mlessons/calculus/apphyper.html) Also, they help the upward air flow move faster, cooling things faster and better.
No comments:
Post a Comment